Tag: hsv

HSV(ish) Colour Wheel in Python

Years back I wrote something about HSV colour cycling for Arduino. Things have moved on: we’re all writing code in MicroPython/CircuitPython now and 8-bit micro-controllers are looking decidedly quaint. Yes, yes; some of you must still write code in PIC assembly language and I’m sure that’s very lovely for you indeed don’t @ me.

If you look at the output of a typical HSV to RGB algorithm, the components map something like this:

Hue between 0-1, with saturation and value set to 1. Output range 0-1 for each component

These lines remind me so much of sine waves, if very blocky ones. The red trace in particular is just the cosine function, with the input range of 0..2Ï€ and the output range of -1..1 both mapped to 0..1. The green and blue traces are just the red trace shifted horizontally by â…“ and â…” respectively.

Since we have transcendental functions in MicroPython, we don’t have to fossick about with linear approximations. The common RGB LED function wheel() uses similar linear interpolation as the graph above. Why make do with blocky cogwheels when you can have a smooth colour wheel?

def cos_wheel(pos):
     # Input a value 0 to 255 to get a colour value.
     # scruss (Stewart Russell) - 2019-03 - CC-BY-SA
     from math import cos, pi
     if pos < 0:
         return (0, 0, 0)
     pos %= 256
     pos /= 255.0
     return (int(255 * (1 + cos( pos            * 2 * pi)) / 2),
             int(255 * (1 + cos((pos - 1 / 3.0) * 2 * pi)) / 2),
             int(255 * (1 + cos((pos - 2 / 3.0) * 2 * pi)) / 2))
Though you never quite get a pure red, green or blue, the results are pleasing

Quite elegant, I thought. Yeah, it may be computationally expensive, but check next year when we’ll all be running even faster µcs. Certainly none of the mystery switch statements or nested conditionals you’ll see in other code. Just maths, doing its thing.

First half is cosine wheel, second half (after red flash) is linear

much improved HSV colour cycling LED on Arduino

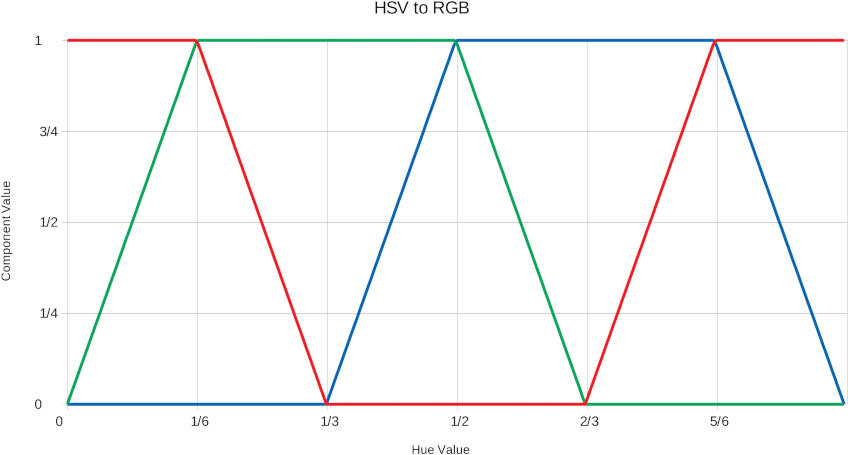
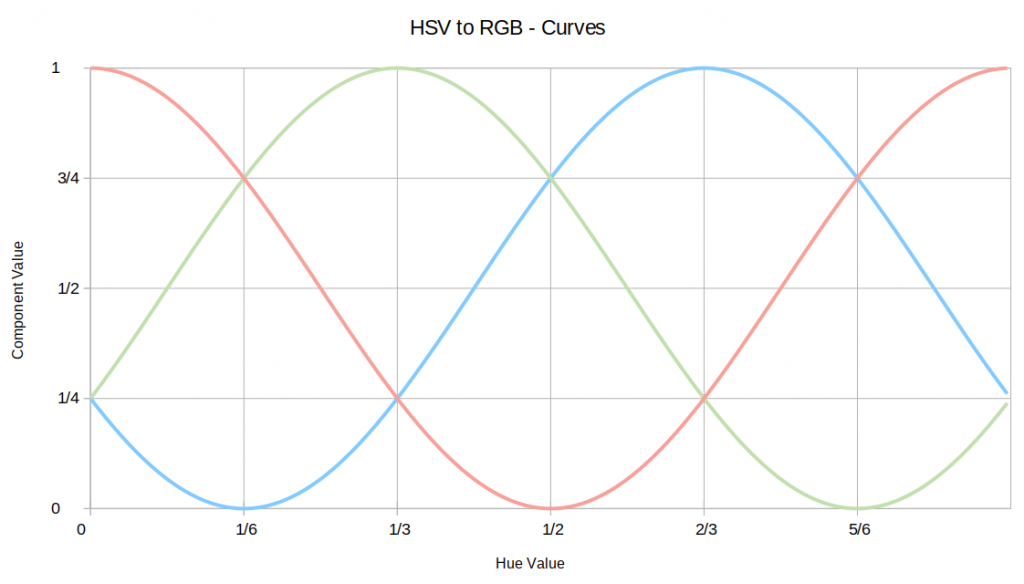
There were some flaws in the post HSV colour cycling LED on Arduino. This does much more what I wanted:

/*
HSV fade/bounce for Arduino - Stewart C. Russell - scruss.com - 2010/09/19

Wiring:
LED is RGB common cathode (SparkFun sku: COM-09264 or equivalent)
    * Digital pin  9 → 165Ω resistor → LED Red pin
    * Digital pin 10 → 100Ω resistor → LED Green pin
    * Digital pin 11 → 100Ω resistor → LED Blue pin
    * GND → LED common cathode.
*/

#define RED                9 // pin for red LED; green on RED+1 pin, blue on RED+2 pin
#define DELAY              2

long rgb[3];
long rgbval, k;
float hsv[3] = {
  0.0, 0.5, 0.5
};
float hsv_min[3] = {
  0.0, 0.0, 0.4 // keep V term greater than 0 for smoothness
};
float hsv_max[3] = {
  6.0, 1.0, 1.0
};
float hsv_delta[3] = {
  0.0005, 0.00013, 0.00011
};

/*
chosen LED SparkFun sku: COM-09264
 has Max Luminosity (RGB): (2800, 6500, 1200)mcd
 so we normalize them all to 1200 mcd -
 R  1200/2800  =  0.428571428571429   =   109/256
 G  1200/6500  =  0.184615384615385   =    47/256
 B  1200/1200  =  1.0                 =   256/256
 */
long bright[3] = {
  109, 47, 256
};

void setup () {
  randomSeed(analogRead(4));
  for (k=0; k<3; k++) {
    pinMode(RED + k, OUTPUT);
    rgb[k]=0; // start with the LED off
    analogWrite(RED + k, rgb[k] * bright[k]/256);
    if (k>1 && random(100) > 50) {
      // randomly twiddle direction of saturation and value increment on startup
      hsv_delta[k] *= -1.0;
    }
  }
}

void loop() {
  for (k=0; k<3; k++) { // for all three HSV values
    hsv[k] += hsv_delta[k];
    if (k<1) { // hue sweeps simply upwards
      if (hsv[k] > hsv_max[k]) {
        hsv[k]=hsv_min[k];
      }    
    }
    else { // saturation or value bounce around
      if (hsv[k] > hsv_max[k] || hsv[k] < hsv_min[k]) {
        hsv_delta[k] *= -1.0;
        hsv[k] += hsv_delta[k];
      }
    }
    hsv[k] = constrain(hsv[k], hsv_min[k], hsv_max[k]); // keep values in range
  }

  rgbval=HSV_to_RGB(hsv[0], hsv[1], hsv[2]);
  rgb[0] = (rgbval & 0x00FF0000) >> 16; // there must be better ways
  rgb[1] = (rgbval & 0x0000FF00) >> 8;
  rgb[2] = rgbval & 0x000000FF;

  for (k=0; k<3; k++) { // for all three RGB values
    analogWrite(RED + k, rgb[k] * bright[k]/256);
  }
  delay(DELAY);
}

long HSV_to_RGB( float h, float s, float v ) {
  /*
     modified from Alvy Ray Smith's site:
   http://www.alvyray.com/Papers/hsv2rgb.htm
   H is given on [0, 6]. S and V are given on [0, 1].
   RGB is returned as a 24-bit long #rrggbb
   */
  int i;
  float m, n, f;

  // not very elegant way of dealing with out of range: return black
  if ((s<0.0) || (s>1.0) || (v<0.0) || (v>1.0)) {
    return 0L;
  }

  if ((h < 0.0) || (h > 6.0)) {
    return long( v * 255 ) + long( v * 255 ) * 256 + long( v * 255 ) * 65536;
  }
  i = floor(h);
  f = h - i;
  if ( !(i&1) ) {
    f = 1 - f; // if i is even
  }
  m = v * (1 - s);
  n = v * (1 - s * f);
  switch (i) {
  case 6:
  case 0: // RETURN_RGB(v, n, m)
    return long(v * 255 ) * 65536 + long( n * 255 ) * 256 + long( m * 255);
  case 1: // RETURN_RGB(n, v, m) 
    return long(n * 255 ) * 65536 + long( v * 255 ) * 256 + long( m * 255);
  case 2:  // RETURN_RGB(m, v, n)
    return long(m * 255 ) * 65536 + long( v * 255 ) * 256 + long( n * 255);
  case 3:  // RETURN_RGB(m, n, v)
    return long(m * 255 ) * 65536 + long( n * 255 ) * 256 + long( v * 255);
  case 4:  // RETURN_RGB(n, m, v)
    return long(n * 255 ) * 65536 + long( m * 255 ) * 256 + long( v * 255);
  case 5:  // RETURN_RGB(v, m, n)
    return long(v * 255 ) * 65536 + long( m * 255 ) * 256 + long( n * 255);
  }
}Â